Предсказание распределения ионов пептида при положительной электроспрейной ионизации

А.И. Воронина*, В.С. Скворцов

Научно-исследовательский институт биомедицинской химии им. В.Н. Ореховича,
119121, Москва, ул. Погодинская, 10; *e-mail: an.voronina@list.ru

Ключевые слова: пептид; масс-спектрометрия; электроспрей; предсказание свойств

DOI: 10.18097/BMCRM00233

ВВЕДЕНИЕ

При протеомном анализе пептидов масс-спектрометрическим (MS) методом [1] с ионизацией электроспреем (ESI), например, при тандемной масс-спектрометрии (MS/MS), количество ионов определённого заряда зависит от используемого оборудования и от условий эксперимента (например, приложенного напряжения, концентрации или скорости потока раствора, состава растворителя) [2]. В то же время распределение ионов при ESI в одних и тех же условиях определяется в первую очередь аминокислотной последовательностью пептида [3]. Возможность предсказания a priory этого распределения может помочь при планировании эксперимента, например, выбрать способ ферментативного гидролиза или диапазон рабочего окна величины m/z для регистрации ионов, отслеживать ионы с определённым зарядом и др. Знать долю от общего количества пептида важно также в экспериментах по количественному определению белка с помощью масс-спектрометрических исследований. Исходные (т.н. «сырые») данные масс-спектрометрических экспериментов, как правило, депонируются на соответствующих ресурсах (например, ProteomeXchange [4]) и могут быть использованы для формирования обучающих выборок большого объёма с целью последующего создания предсказательных моделей с использованием широкого спектра методов, включая и методы машинного обучения.

Ранее нами был построен набор уравнений линейной регрессии, с использованием которых можно предсказать долю ионов 1+, 2+ и 3+ для произвольного пептида [3]. При этом было показано, что соотношение долей пептида между ионами разного заряда не зависит от концентрации пептида в экспериментальной пробе. В данной работе были использованы три выборки большего размера, сформированные на основе исходных данных, полученных разными группами исследователей [5-7], и проанализирована возможность создания предсказательных моделей с использованием нейронных сетей.

МЕТОДИКА

Важным условием данной работы было наличие данных с большим числом повторов, полученных на однотипном оборудовании. В связи с этим мы использовали три набора данных (LC-MS/MS), депонированных в ProteomeXchange: PXD032141 (выборка 1, 11166 пептидов) [5] – 72 пробы, данные получены на тканях домашней мыши (Mus musculus), MS анализ выполнен на масс-спектрометре Orbitrap Fusion Lumos™ Tribrid (“Thermo Scientific”, США); PXD051750 (выборка 2, 17073 пептида) [6] – 36 проб, данные получены на тканях мыши (Mus musculus), MS анализ выполнен на Q Exactive HF (“Thermo Scientific”); PXD019263 (выборка 3, 21463 пептида) [7] – 21 проба (по 3 технических повтора), данные получены на линии клеток HepG2 (Homo sapiens), MS анализ выполнен на Q Exactive HF.

Данные авторов [5-7] по идентификации пептидов для всех трёх выборок не использовали, а процедуру идентификации провели заново. Выборки 1 и 2 уже были использованы в наших работах ранее [8, 9]. Идентификацию пептидов для выборки 3 проводили независимо для каждой пробы по той же схеме [8, 9] со следующими параметрами: 2 ppm для первичных ионов и 0.01 Да для ионов фрагментов, уровень ложноположительных результатов (false discovery rate, FDR) – 0.01%. Данные для пептидов с посттрансляционными модификациями не использовали. Выравнивание всего пространства первичных ионов и нормализация величины площади под пиком для каждого из первичных ионов (Normalized abundance, NA) проводили средствами программы Progenesis LC-MS [10].

Для каждого идентифицированного пептида формировали спектр зарядовых состояний (использовали ионы с зарядом от 1+ до 5+) по каждой из проб. Критериями совпадения пиков LC-MS были: различие по массе пептида не более 1 ppm; максимальное пересечение диапазона времени удержания (не менее 50%); в спорных случаях, если данным условиям соответствовали более одного варианта, отбирали вариант с большей величиной NA. Разброс значений NA был ограничен 3 порядками от максимально наблюдаемого значения, значения меньше данного порога обнулялись. Сумма значений NA по всем ионам для конкретного пептида не должна была быть меньше 10000, иначе пептиды исключали из выборки. Из всего набора биологических проб отбирали варианты, в которых было наибольшее число зарядных состояний, после чего вычисляли долевое значение каждого зарядного состояния в пробе и усредняли по всем отобранным пробам. Если в пробах был зарегистрирован только один ион, но с разным зарядовым состоянием для разных биологических проб, распределение между ионами считали равномерным, при условии, если количество ионов одного состояния было не менее 25% другого. В противном случае считали, что ионы пептида встречаются только в одном состоянии (в том, для которого наблюдений было больше).

Все вычисления проводили с использованием собственной программы, написанной на языке Python. Для работы с нейронными сетями использовали библиотеку PyTorch.

Для анализа в качестве набора предсказываемых (независимых) величин использовали набор долевых значений для каждого варианта (класса) иона от 1+ до 5+ (в сумме 1). В качестве независимых переменных для каждого пептида рассчитывали набор параметров в нескольких вариантах:

1. SP60 – вектор из 60 значений. Первые 20 чисел – значение “1” для порядкового номера (порядок остатков при расчёте: W, F, L, I, M, V, Y, A, T, P, E, D, C, S, Q, G, N, R, H, K) первого аминокислотного остатка, для остальных “0”, аналогично для диапазона с 41 по 60 – учитывается C-концевой аминокислотный остаток, для диапазона 21-40 каждое число – частота встречаемости аминокислотных остатков для фрагмента со 2-го по предпоследний остаток.
2. pkAB – вектор из 34 значений. Последовательно записываются 14 характеристик пептида: длина пептида, масса пептида, 6 наибольших значений 14-pKa, 6 наибольших значений pKb (если диссоциируемых или протонируемых групп меньше 6 – значение для незанятых позиций “0”), 20 оставшихся значений – частота встречаемости аминокислотных остатков в пептиде (порядок остатков как в предыдущем).
3. L64P31 – матрица 64x31, каждый из аминокислотных остатков в последовательности описывается 31 характеристикой с использованием 11 табличных значений для каждого остатка (молекулярный вес, pI, pKa, pKb, объём, гидрофобность и др.) и 20 бинарными значениями, определяющими аминокислотный остаток согласно описанию программы ProteinCNN [11]. Максимальная длина пептида 64 аминокислотных остатка, незаполненный остаток обнуляется.
4. TNE – тензор 64х64, формирующийся на основании порядковых номеров и типов аминокислотных остатков с помощью модуля torch.nn.Embedding пакета PyTorch [12]. Максимальная длина пептида 64 аминокислотных остатка.

Конфигурацию нейронных сетей также варьировали. В каждом случае, использовали не менее 4 последовательных слоёв с функцией активации ReLU для входного и скрытых слоёв, для выходного слоя варьировали функцию активации: sigmoid для предсказания доли иона соответствующего заряда независимо от других классов (сумма предсказанных значений могла отличаться от 1); softmax для предсказания долевого распределения между классами (сумма предсказанных значений равна 1). Также варьировали функцию потерь, использовали либо кросс-энтропию (CrossEntr), либо среднеквадратичную ошибку (MSE). В каждом случае проводили по 100 циклов обучения.

Всего тестировали 4 варианта:

1. CONV1D - 3 конволюционных слоя с обработкой данных 1D (16, 64, 128 нейронов (v1) при использовании входных данных вариантов SP60 и pkAB, 128, 256, 512 (v2) в остальных случаях), 2 линейных слоя (500 и 5 нейронов);
2. CONV2D - 3 конволюционных слоя с обработкой данных 2D (16, 64, 128 нейронов), 2 линейных слоя (500 и 5 нейронов);
3. RNN - рекуррентная нейронная сеть с модулем памяти LSTM; 4 линейных слоя (128, 256, 512 и 5 нейронов);
4. LINEAR - 4 линейных слоя (128, 256, 512 и 5 нейронов).

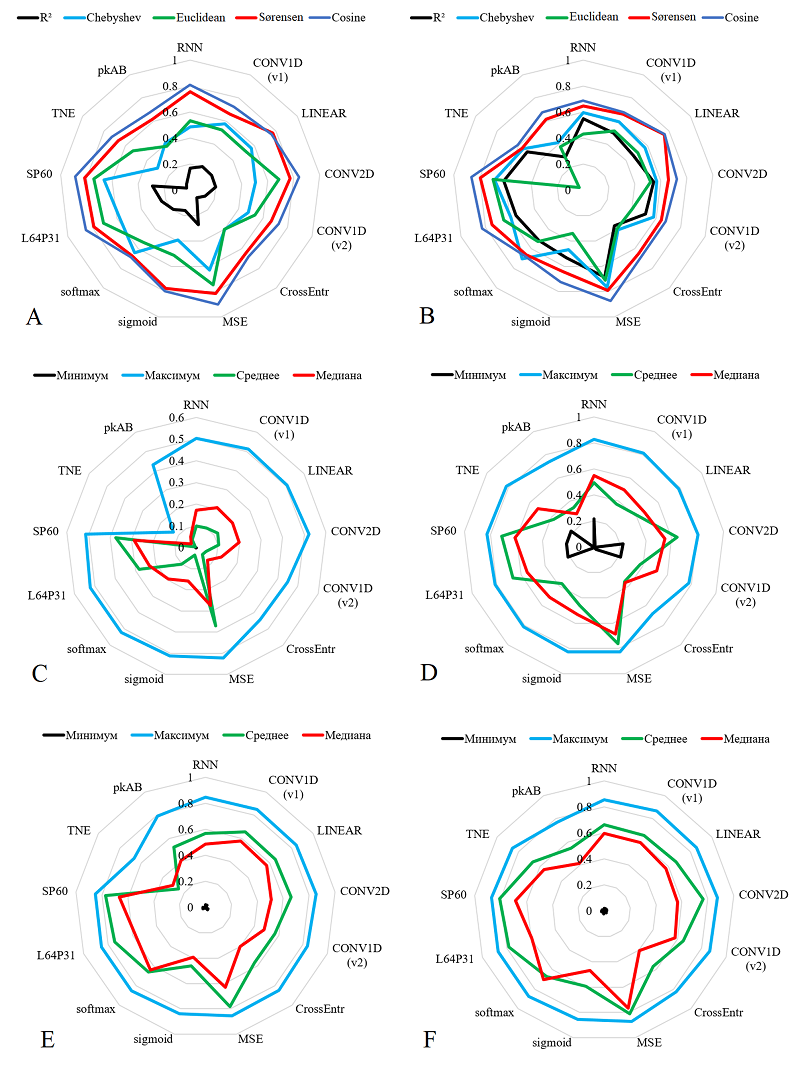
Для обучения нейронных сетей для каждой из трёх выборок случайным образом выделяли 70% как обучающую выборку и 30% как тестовую (повторяли 2 раза). После обучения дополнительно проводили предсказание величин для двух других выборок. Как меру качества предсказания рассматривали коэффициент детерминации (R²) и набор метрик Euclidean, Srensen, Chebyshev, Cosine.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Всего было построено 128 нейронных сетей (64 комбинаторных варианта). Результаты тестирования для 30% тестовых (A, 128 вариантов) и независимых выборок (Б, 256 вариантов) рассматривали по отдельности. Ожидаемо, результаты первой группы несколько лучше. На рисунке 1 представлены примеры лепестковых гистограмм распределения максимальных, минимальных, средних и медианных значений использованных метрик, сгруппированных по отдельным характеристикам построенных нейронных сетей (т.е. в выделенной группе одна из характеристик совпадает). Так как для трёх из используемых метрик (Euclidean, Srensen, Chebyshev) лучшее значение 0, а для других двух 1, то для наглядности на графиках для этих метрик используется величина “1 - значение метрики”. Таким образом, для всех метрик на гистограммах наилучшее значение 1. Максимальные и минимальные значения метрик для каждой из групп не дают возможности выбрать лучшую группу вариантов, хотя и позволяют выбрать лучшие варианты конкретных нейронных сетей. Медианное значение для этого подходит лучше, особенно в случае, если оно превышает среднее значение. Видно, что наибольшие различия имеют оценки качества модели с использованием метрики Chebyshev и коэффициента детерминации. Наилучшие результаты показывают нейронные сети архитектуры CONV1D и в меньшей степени RNN, функция активации sigmoid, функция потерь MSE. Ещё большее значение имеет структура входных данных: варианты SP60 и L64P31 выигрывают с существенным отрывом. Важно отметить, что оба варианта содержат (помимо прочих характеристик) спектр аминокислотных остатков. Вариант pkAB частично совпадает по физико-химическим характеристикам пептида с частью данных из варианта L64P31, но сами табличные значения взяты из другого источника. Вариант представления данных TNE оказался малопригоден для решения данной задачи.

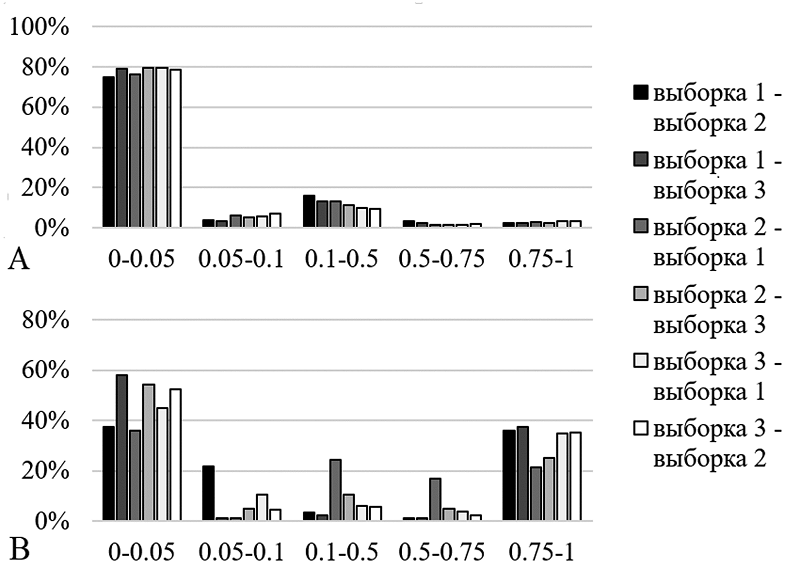
На рисунке 2A представлена гистограмма распределения абсолютного значения ошибки предсказания для нейронных сетей, отобранных по лучшим значениям медианы для метрики Chebyshev (RNN, sigmoid, MSE, SP60) для независимых тестовых выборок. Для каждого из вариантов не менее чем в 80% случаев ошибка не превышает 0.1 (теоретически возможное значение ошибки от 0 до 1). Для сравнения приведена аналогичная гистограмма для варианта представления данных TNE (рис. 2B).

Данной точности недостаточно для коррекции данных при определении концентрации белков безметковым (label-free) методом [3]. В то же время данной точности достаточно при планировании протеомного эксперимента, когда нужно подобрать условия, при которых будет детектироваться максимально возможное число пептидов конкретных белков, важных для исследователя.

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

Данная работа не включает исследования, в которых в качестве объекта выступали люди или животные.

ФИНАНСИРОВАНИЕ

Работа выполнена в рамках Программы фундаментальных научных исследований в Российской Федерации на долгосрочный период (2021-2030 годы) (№ 122030100170-5).

КОНФЛИКТ ИНТЕРЕСОВ

Авторы заявляют об отсутствии конфликта интересов.

ЛИТЕРАТУРА

1. Yates, J.R., Ruse, C.I., Nakorchevsky, A. (2009) Proteomics by mass spectrometry: approaches, advances, and applications. Annu. Rev. Biomed. Eng., 11, 49–79. DOI
2. Iavarone, A.T., Jurchen, J.C., Williams, E.R. (2000) Effects of solvent on the maximum charge state and charge state distribution of protein ions produced by electrospray ionization. J. Am. Soc. Mass Spectrom., 11(11), 976–985. DOI
3. Skvortsov, V.S., Alekseychuk, N.N., Miroshnichenko, Y.V., Rybina, A.V. (2019) The prediction of the ion fraction of the peptide with selected charge in mass spectrometry with positive electrospray ionization. Biomedical Chemistry: Research and Methods, 2(4), e00100. DOI
4. ProteomeXchange. Retrieved July 20, 2024, from: https://proteomecentral.proteomexchange.org
5. Ramiro, L., Faura, J., Simats, A., García-Rodríguez, P., Ma, F., Martín, L., Canals, F., Rosell, A., Montaner, J. (2023) Influence of sex, age and diabetes on brain transcriptome and proteome modifications following cerebral ischemia. BMC Neurosci., 24(1), 7. DOI
6. Proteomics identification database, project PXD051750. DOI
7. Vavilov, N.E., Zgoda, V.G., Tikhonova, O.V., Farafonova, T.E., Shushkova, N.A., Novikova, S.E., Yarygin, K.N., Radko, S.P., Ilgisonis, E.V., Ponomarenko, E.A., Lisitsa, A.V., Archakov, A.I. (2020) Proteomic analysis of Chr 18 proteins using 2D fractionation. J. Proteome Res, 19(12), 4901–4906. DOI
8. Voronina, A.I., Miroshnichenko, Yu.V., Skvortsov, V.S. (2024) Bioinformatic identification of proteins with altered PTM levels in a mouse line established to study the mechanisms of the development of fibromuscular dysplasia. Biomeditsinskaya Khimiya, 70(4), 248–255. DOI
9. Rybina, A.V. (2024) Identification of proteoforms in experimental ischemic stroke in mice: Comparison of data from 2D electrophoresis and an independent experiment with mass spectrometric identification. Proceedings Book of the XXX Symposium “Bioinformatics and Computer-Aided Drug Discovery”, 116. DOI
10. Progenesis LC-MS version 4.0, Nonlinear Dynamics, Newcastle upon Tyne, UK.
11. ProteinCNN. Retrieved July 20, 2024, from: https://github.com/rwalroth/ProteinCNN
12. Li, Z., Yu, Y. (2016) Protein secondary structure prediction using cascaded convolutional and recurrent neural networks. arXiv preprint 1604.07176. DOI