Выравнивание и нормирование данных масс-спектрометрических экспериментов с использованием индекса гидрофобности

В.С. Скворцов, А.И. Воронина*, А.В. Рыбина

Научно-исследовательский институт биомедицинской химии имени В.Н. Ореховича, 119121, Москва, ул. Погодинская, 10; *эл. почта: an.voronina@list.ru

Ключевые слова: время удержания; масс-спектрометрия; выравнивание данных

DOI: 10.18097/BMCRM00245

ВВЕДЕНИЕ

В настоящее время жидкостная хроматография (ЖК), сопряженная с масс-спектрометрией (ЖХ-МС) или тандемной масс-спектрометрией (ЖХ-МС/MC), стала важным инструментом протеомного и метаболомного анализа сложных образцов [1]. Однако существенной проблемой при сравнении результатов нескольких измерений ЖХ-МС, как в технических повторах, проводимых для повышения надежности идентификации, так и в случае анализа нескольких биологических образцов, является вариабельность времени удерживания (RT) в разных экспериментах. Данные ЖХ подвержены влиянию большого числа внешних факторов, в том числе таких, как качество пробоподготовки, незначительных отклонений в настройках оборудования, колебание давления, изменение температуры колонки или подвижной фазы, а иногда и различия в анализируемых пробах. Вариабельность RT на хроматографической колонке встречается во всех наборах данных, поэтому для корректного сравнения образцов часто необходимо скорректировать искажения по RT. Это также важно для обработки данных для количественной безметочной протеомики (ЖХ-МС/MC), когда требуется нормализация данных по интенсивности сигнала [2, 3]. Существует несколько подходов к решению данной проблемы. Первый включает сравнение карт ЖХ-МС на уровне необработанных данных [4] с помощью методов многостороннего анализа данных. Несмотря на то, что эта группа алгоритмов позволяет выявлять  дифференциально экспрессированные белки, к недостаткам данного подхода следует отнести большое время работы, невозможность выравнивания для сильно отличающихся биологических проб [1] или разных фракций при многомерном ЖХ-МС разделении и тот факт, что алгоритмы обычно описываются для парного выравнивания. Другой подход – выравнивание карт признаков в ЖХ-МС [1]. Принципиально это очень близкий подход, однако  он предусматривает использование не всей совокупности данных, а карты признаков, сгруппированных по заданным параметрам. При этом могут корректироваться как линейные, так и нелинейные искажения величины RT по всем картам признаков. Этот подход широко используется, например, в программах msInspect, MZmine , OpenMS и XCMS и др. [1]. Несмотря на свою быстроту, он требует предварительной обработки данных, а используемые для этого алгоритмы также могут вносить собственные ошибки. Как и предыдущий подход, анализ карт признаков использует данные только ЖХ-МС и так же сильно зависит от сходства между наборами данных ЖХ-МС.

Существует и альтернативный метод, объединяющий информацию, полученную с помощью ЖХ-МС, с информацией, полученной с помощью МС/МС [5]. В этом варианте МС/МС-спектры с уверенно идентифицированными пептидными последовательностями представляют собой эталон, относительно которого данные ЖХ-МС(/МС) могут быть выравнены. Считается, что данный подход даёт недостаточно точное выравнивание, и иногда его используют как первый этап (предварительное выравнивание), дополняя затем процедурами, относящимися к первым двум вариантам [6-8]. Основное преимущество данного варианта – возможность выравнивать наборы данных, которые имеют большие различия, например, отдельные фракции после многомерного разделения [5]. Также следует отметить, что точность выравниванияв в этом варианте достаточна для решения широкого спектра задач, например, для контроля ложных идентификаций или сравнения количества конкретного пептида в различных пробах. Последнее также требует нормализации данных в различных пробах по интенсивности сигнала, первым этапом для чего также необходимо выравнивание по RT. Описанные в данной статье алгоритм и программа используют именно этот вариант выравнивания.

МЕТОДИКА

В работе использованы 2 набора данных ЖХ-МС/МС. Первый взят из работы [9], в которой моделировали ишемию головного мозга с использованием окклюзии средней мозговой артерии. Исходные данные работы [9] доступны в базе данных ProteomeXchange [10] (accession code PXD032141). Использовали только набор данных для молодых самцов мышей с диабетом (выборка 1: всего 24 пробы, 8 из зоны инфаркта мозга, 8 из другого полушария мозга и 8 контрольных, по 4 из разных полушарий мозга). Второй – данные, полученные в работе [11] (accession code PXD000065), в которой для анализа белков клеточной линии A431 был использован метод фракционирования пептидов с использованием изоэлектрического фокусирования (HiRIEF). Использовали часть данных для немодифицированных пептидов, полученных в диапазоне pH от 3 до 10 (выборка 2: 72 пробы с шагом в ~0.1 значения pH). В обоих случаях идентификация пептидов была проведена заново средствами программы PEAKS Studio [12] (погрешность идентификации для первичных ионов 10 ppm и 0.02 Da для вторичных ионов, уровень False Discovery Rate (FDR) - 1%). Каждую пробу анализировали независимо. В качестве входных файлов для последующего анализа использовали файлы экспорта PEAKS Studio “peptide features” (PF).

В качестве набора «эталонных» пептидов использовали часть обучающей выборки программы Chronologer [13], в свою очередь взятую авторами из работы [14]. Из данного набора были удалены все пептиды с модификациями и пептиды короче 9 аминокислотных остатков и больше 50. В окончательный набор вошло 364232 пептида с диапазоном значений величины индекса гидрофобности HI (Hydrophobicity Index) от -0.07 до 31 (в шкале «Prosit RT» [15]: от -36.5 до 169.5). В работе использовали величину HI, так  как именно её предсказывает программа Chronologer. В случае, если в «эталонном» наборе недостаточно пептидов, совпадающих с исследуемым набором, то можно сформировать новый набор пептидов, относительно которого будет проводиться выравнивание, с использованием предсказанных программой Chronologer величин HI. Также можно использовать и нашу программу RTP [16], предсказывающую ту же величину, но в отличие от Chronologer, использующую простую аддитивную схему расчёта, а не нейронные сети. При аддитивной схеме расчёта средняя ошибка предсказания больше, чем при использовании нейронных сетей, но вероятность случайного выброса очень низкая. При любом варианте предсказания, чем больше пептидов в эталонном наборе, тем меньше влияние ошибки предсказания на конечный результат. При работе с данными, полученными на млекопитающих, должно хватать и имеющегося набора с экспериментальными данными (табл. 1).

Закрыть окно ОТКРЫТЬ В ПОЛНОМ РАЗМЕРЕ

Таблица 1. Число пептидов, полученных в ходе виртуального расщепления трипсином, которые теоретически могут совпасть с «эталонным» набором для разных биологических видов.

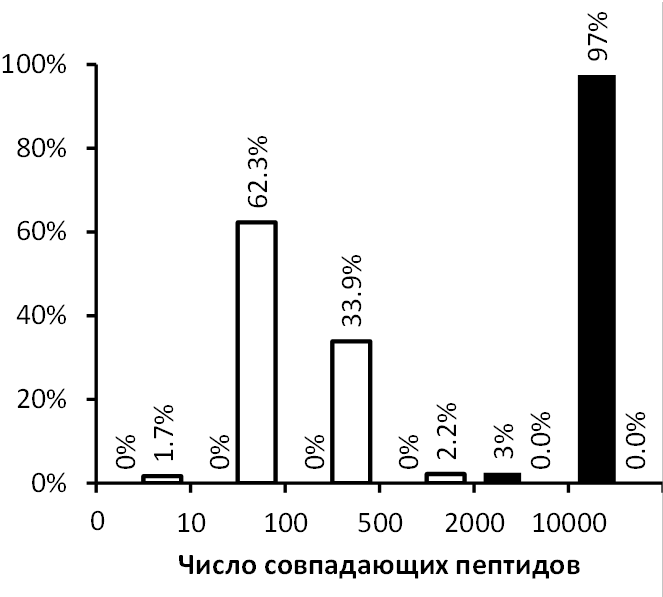
Алгоритм вычислений, описанный ниже, имплементирован в программу, написанную на язык Python (версия 3.6.8) и свободно доступную по адресу http://lpcit.ibmc.msk.ru/AlignRT.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Выравнивание данных относительно «эталонного» набора.

Строго говоря, для выборки 1 (как и в других подобных случаях, когда данные получены на одной конкретной ткани, пусть и для различных условий) в качестве эталона можно использовать данные любой из собственных проб выборки, так как любые 2 пары проб включают в себя не менее нескольких тысяч совпадающих пептидов (рис. 1), относительно равномерно распределённых по значениям RT. Как правило, так и делают. В таком случае использование универсального стандарта полезно для последующего сравнение с данными, полученными на образцах других тканей. Причём сравнивать можно сразу много наборов без дополнительных попарных или множественных выравниваний. В тоже время для выборки 2 число попарных совпадений пептидов тем меньше, чем больше пробы отличаются по значению pH, в 2/3 случаев это несколько десятков пептидов (рис. 1), распределённых неравномерно, и без использования набора «эталонных» пептидов получить адекватное выравнивание всего набора не получится.

Программа выравнивания работает по следующему алгоритму.

1. В качестве файлов входных данных программа использует файл PF, экспортированный из программы PEAKS Studio. Это может быть как один общий файл, в котором принадлежность к пробе индексирована в соответствующей колонке, так и несколько отдельных файлов данных для каждой пробы. Файл PF представляет собой обычный текстовый файл в CSV формате, так что пользователь может использовать и любой другой файл в CSV формате, если он содержит необходимую информацию: значение m/z иона, заряда иона, идентифицированную последовательность пептида, значение максимума RT, значение «аbundance» (либо значение интенсивности), величину характеризующую качество идентификации (для PEAKS Studio это «-10LgP»). После переименования заголовков, такие данные также могут быть использованы.
2. Опционально может быть проведена фильтрация данных по величине «-10LgP». В случае, если используются результаты работы программы PEAKS Studio, и идентификацию для различных проб проводили независимо, то одному и тому же уровню FDR будут соответствовать различные значения величины «‑10LgP». Выравнивание лучше проводить по максимально достоверно идентифицированным пептидам. Например, в примерах для данной работы использовали пептиды с величиной «-10LgP» не менее 30. Это ограничение относилось только к пептидам, использованным для выравнивания; последующий расчёт значений HI проводится для всех пептидов в файле, кроме тех, для которых значения RT выпадают из доверительного интервала (см. далее).
3. Для каждой пробы был определен набор пептидов, совпадающих c «эталонным» набором. На рисунках 2А (выборка 1) и 2B (выборка 2) видно, что даже после фильтрации имеется существенное число наблюдений, для которых значения RT и HI выпадают из общей тенденции даже с учётом зашумлённости данных. Это связано с тем, что имели место ошибки идентификации (либо в нашем случае, либо в работе [14]). Наличия некоторого количества ошибок идентификации избежать практически нельзя. Чтобы нивелировать влияние ошибочных идентификаций процедуру подбора уравнений для пересчёта значений RT в HI проводят итерационно, удаляя по 1% наблюдений с наибольшей ошибкой до максимально возможного значения, установленного пользователем (в нашем примере до 5%). Также из рисунка видно, что если зависимость RT от HI для набора 1 имеет скорее линейный характер, то в случае выборки 2 зависимость явно нелинейная. Программа вычисляет как уравнение линейной зависимости, так и 4 уравнения многочлена от 2 до 5 порядка. Лучший вариант уравнения программа выбирает по величине среднеквадратичной ошибки, причём, если разница между ошибками меньше 5%, то выбирается уравнение с меньшей степенью. При этом программой также устанавливаются значения границ доверительного интервала для наблюдаемого RT (рис. 2C). Для линейных уравнений они определяются по минимальному и максимальному значению HI в выборке, по которой построено уравнение. Для нелинейных уравнений это точки экстремумов в минимуме и максимуме вычисленной величины HI. Выбор уравнения также может быть сделан пользователем. Экстраполяция данных возможна в случае использования линейных уравнений, но при этом велика вероятность, что линейна зависимость HI и RT за пределами доверительных интервалов нарушается.
4. Для всех ионов пептидов, у которых значения RT находятся в пределах доверительного интервала, по выбранным уравнениям производится расчёт значений HI. В этот список входят и те пептиды по которым строили уравнение для пересчёта. Таким образом, порядок следования пептидов по величине RT (HI) в каждой конкретной пробе сохраняется. Границы доверительных интервалов для разных проб могут не совпадать, поэтому для дальнейшего анализа следует выбрать область пересечения доверительных интервалов для всех проб. Однако это зависит от цели, для которой выполняли выравнивание. Например, при объединении данных в единый массив при создании объединённого виртуального «суперспектра» такое ограничение вводить не нужно (пример сравнения выравненных значений HI для отдельных проб представлен на рисунке 2D).

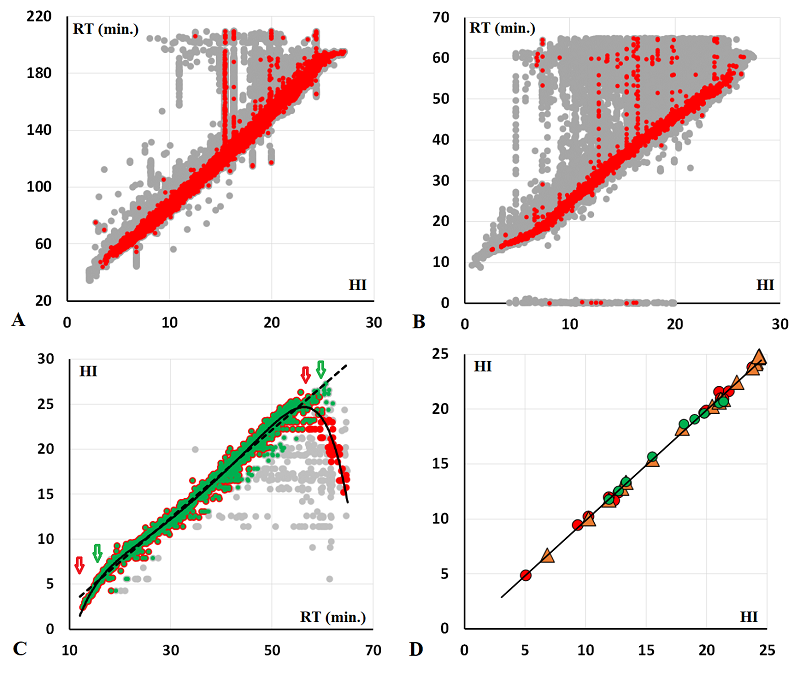
В результате программа формирует набор файлов (для каждой пробы), в которых значения RT (а также RT_min и RT_max, если они указаны) заменены соответственно на HI (HI_min и HI_max). Если в файле присутствовали строки, описывающие ионы, для которых не были идентифицированы пептиды, то для них также проводится перерасчёт значений RT в HI. Остальные данные переносятся из исходного файла без изменений.

Объединение выровненных PF всех проб набора данных в единый файл

При объединении данных результаты идентификации пептидов фиксируются в выходном файле, но не используются для самой процедуры объединения. В первую очередь программа фиксирует значение m/z иона и отбирает все ионы, отличающиеся не более чем на 0.5 ppm (параметр может варьироваться пользователем). Затем проверяется спопарное совпадение диапазонов HI_min - HI_max. Диапазоны считаются совпадающими, если один из них полностью перекрывает второй, либо пересечение составляет не менее 50%, а отклонение величины HI (соответствующей максимуму пика) не превышает 0.1. В выходной файл для каждого иона сохраняются параметры самого иона (m/z, заряд, HI, HI_min, HI_max, все величины кроме заряда усредняются), для каждой пробы формируется отдельная колонка с величиной, указанной пользователем (Area (или abundance) в нашем случае). Для каждой пробы фиксируется, был ли идентифицирован пептид в данной пробе. Если да, то приводится номер пептида из списка, также записываемого в данной строке. Если идентификация неоднозначная, то первым сохраняется вариант пептида, встречающийся чаще.

Нормализация данных по величине abundance

В настоящее время процедура нормализации реализована только для случая, соответствующего набору данных 1, когда для существенной части белков не должно меняться их количество от пробы к пробе. В таком случае каждый конкретный вариант иона для конкретного пептида не должен менять величину интенсивности при измерении кроме как в зависимости от состояния или калибровки аппаратной части. Зная усреднённые значения колебания интенсивности (или abundance, так как эти величины хорошо коррелируют) между пробами, можно нормировать данные для всех проб.

Существует два способа определения выборки данных, по которой можно рассчитать коэффициенты, корректирующие интенсивность сигнала для разных проб. Самый простой – установить список белков, количество которых не меняется в зависимости от изменения условий, данных в эксперименте. Второй вариант – определить группу данных изменяющих значения интенсивности (или abundance) сходным образом. Группа, включающая в себя большую часть пептидов, очевидно, характеризует именно группу консервативных белков.

Так как белки представлены в пробах в различном (и неизвестным заранее) количестве, то для того чтобы построить кластеры ионов пептидов со схожим распределением по пробам, требуется провести нормирование данных для каждого наблюдаемого иона. Для этого использовали следующую формулу:

F_norm = (F_i – F_med)/(F_med),

где F_norm – нормализованное значение величины интенсивности (или abundance) для иона пептида из i-той пробы; F_i – актуальное значение той же величины для i-той пробы; F_med – среднее значение той же величины по всем (в данном случае 24) пробам. В данной работе для отбора кластера наибольшего размера и вычисления множителей для нормализации использовали только ионы пептидов заряда 2+, идентифицированные во всех 24 пробах набора 1 (рис. 3). Всего таких ионов было 4200. В качестве меры сходства использовали значение попарного квадрата коэффициента детерминации, пороговое значения установили равным 0.75. Всего в отобранный кластер ионов вошло 2400 значений.

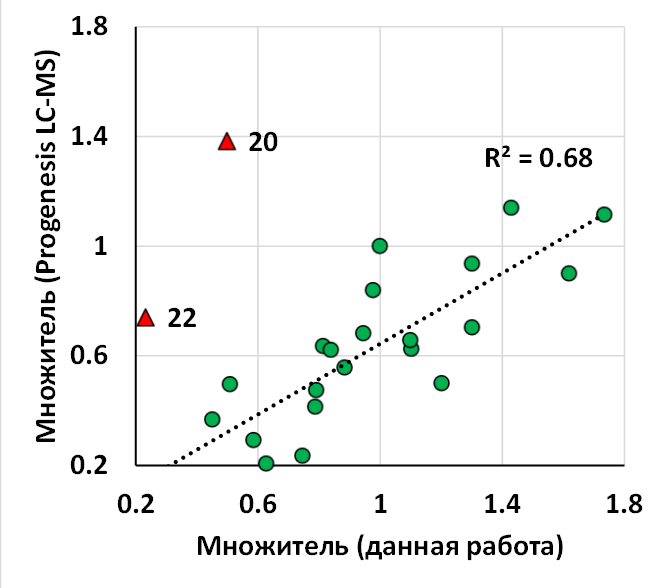
В работе [17] для набора 1 была проведена нормализация величины abundance с использованием программы Progenesis LC-MS [18]. На рисунке 4 приведено сравнение множителей для нормализации, полученных в данной работе и в работе [17]. Видно, что пробы 20 и 22 выпадают из общего тренда, однако, множители для нормализации остальных проб хорошо коррелируют между собой (R² = 0.68).

Таким образом, представленная программа позволяет выравнивать по RT любые наборы масс-спектрометрических данных, в независимости от того, насколько они похожи по пептидному составу и количеству вещества. При этом можно отследить наличие специфических ионов и оценить их относительное количество в различных пробах. В части случаев программа позволяет провести нормализацию величины abundance, что даёт возможность делать более точные оценки при количественном анализе.

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

Данная работа не содержит каких-либо исследований с использованием людей и животных в качестве объектов исследования.

ФИНАНСИРОВАНИЕ

Работа выполнена в рамках Программы фундаментальных научных исследований в Российской Федерации на долгосрочный период (2021 - 2030 годы) (№ 122030100170-5).

КОНФЛИКТ ИНТЕРЕСОВ

Авторы заявляют об отсутствии конфликта интересов.

ЛИТЕРАТУРА

1. Lange, E., Tautenhahn, R., Neumann, S., Gröpl, C. (2008) Critical assessment of alignment procedures for LC-MS proteomics and metabolomics measurements. BMC Bioinformatics, 9, 375. DOI
2. Ong, S.E., Mann, M. (2005) Mass spectrometry-based proteomics turns quantitative. Nature Chemical Biology, 1(5), 252-262. DOI
3. Ong, S.E., Foster, L.J., Mann, M. (2003) Mass spectrometric-based approaches in quantitative proteomics. Methods (San Diego, Calif.), 29(2), 124-130. DOI
4. Vandenbogaert, M., Li-Thiao-Té, S., Kaltenbach, H.M., Zhang, R., Aittokallio, T., Schwikowski, B. (2008) Alignment of LC-MS images, with applications to biomarker discovery and protein identification. Proteomics, 8(4), 650-672. DOI
5. America, A.H., Cordewener, J.H. (2008) Comparative LC-MS: a landscape of peaks and valleys. Proteomics, 8(4), 731-749. DOI
6. Fischer, B., Grossmann, J., Roth, V., Gruissem, W., Baginsky, S., Buhmann, J.M. (2006) Semi-supervised LC/MS alignment for differential proteomics. Bioinformatics, 22(14), e132-140. DOI
7. Jaffe, J.D., Mani, D.R., Leptos, K.C., Church, G.M., Gillette, M.A., Carr, S.A. (2006) PEPPeR, a platform for experimental proteomic pattern recognition. Molecular & Cellular Proteomics, 5(10), 1927-1941. DOI
8. Prince, J.T., Marcotte, E.M. (2006) Chromatographic alignment of ESI-LC-MS proteomics data sets by ordered bijective interpolated warping. Analytical Chemistry, 78(17), 6140-6152. DOI
9. Ramiro, L., Faura, J., Simats, A., García-Rodríguez, P., Ma, F., Martín, L., Canals, F., Rosell, A., Montaner, J. (2023) Influence of sex, age and diabetes on brain transcriptome and proteome modifications following cerebral ischemia. BMC Neuroscience, 24(1), 7. DOI
10. ProteomeXchange, project PXD051750. Retrieved January 29, 2025, from: http://central.proteomexchange.org/cgi/GetDataset?ID=PXD051750 DOI
11. Branca, R., Orre, L., Johansson, H., Granholm, V., Huss, M., Pérez-Bercoff, A., Forshed, J., Käll, L., Lehtiö, J. (2014) HiRIEF LC-MS enables deep proteome coverage and unbiased proteogenomics. Nature Methods, 11, 59-62. DOI
12. Xin, L., Qiao, R., Chen, X., Tran, H., Pan, S., Rabinoviz, S., Bian, H., He, X., Morse, B., Shan, B., Li, M. (2022) A streamlined platform for analyzing tera-scale DDA and DIA mass spectrometry data enables highly sensitive immunopeptidomics. Nature Communications, 13, 3108. DOI
13. Wilburn, D.B., Shannon, A.E., Spicer, V., Richards, A.L., Yeung, D., Swaney, D.L., Krokhin, O.V., Searle, B.C. (2023) Deep learning from harmonized peptide libraries enables retention time prediction of diverse post translational modifications, bioRxiv, 5(30), 542978. DOI
14. Wilhelm, M., Zolg, D.P., Graber, M., Gessulat, S., Schmidt, T., Schnatbaum, K., Schwencke-Westphal, C., Seifert, P., de Andrade Krätzig, N., Zerweck, J., Knaute, T., Bräunlein, E., Samaras, P., Lautenbacher, L., Klaeger, S., Wenschuh, H., Rad, R., Delanghe, B., Huhmer, A., Carr, S.A., Clauser, K.R., Krackhardt, A.M., Reimer, U., Kuster, B. (2021) Deep learning boosts sensitivity of mass spectrometry-based immunopeptidomics. Nature Communications, 12, 3346. DOI
15. Gessulat, S., Schmidt, T., Zolg, D.P., Samaras, P., Schnatbaum, K., Zerweck, J., Knaute, T., Rechenberger, J., Delanghe, B., Huhmer, A., Reimer, U., Ehrlich, H.C., Aiche, S., Kuster, B., Wilhelm, M. (2019) Prosit: proteome-wide prediction of peptide tandem mass spectra by deep learning. Nature Methods, 16(6), 509-518. DOI
16. Voronina, A.I., Rybina, A.V. (2023) A Program for Predicting the Retention Time of Peptides with Post-Translational Modifications. Biomedical Chemistry: Research and Methods, 6(3), e00196. DOI
17. Rybina, A.V. (2024) Identification of mouse brain proteoforms: comparison of 2D-electrophoresis data and independent experiment with mass spectrometric identification. Biomeditsinskaya Khimiya, 70(6), 475-480. DOI
18. Progenesis LC-MS version 4.0, Nonlinear Dynamics, Newcastle upon Tyne, UK.