К 40-летию Института физиологически активных веществ РАН
|
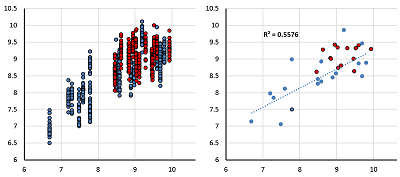
СОДЕРЖАНИЕ Рисунок 3 Предсказание выборки 2 (красный) по модели, обученной на выборке 1 (синий). Рецептор M3. Таблица 1 Структуры ацетилхолиновых мускариновых рецепторов, представленные в PDB. Таблица 2 Антагонисты ацетилхолиновых мускариновых рецепторов. Таблица 3 Показатели обучения моделей линейной регрессии по отдельным рецепторам. Таблица 4 Предсказательная способность моделей при кросс-рецепторном предсказании (R2). |
Компьютерная оценка селективности ингибирования
1Институт физиологически активных веществ Российской академии наук
142432 Черноголовка Московской обл., Северный проезд, 1;
*e-mail: a.v.mikurova@ibmc.msk.ru Ключевые слова: мускариновые ацетилхолиновые рецепторы; ингибиторы; конкурентное ингибирование; докинг; вычислительные методы; молекулярная динамика; QSAR DOI: 10.18097/BMCRM00072 ВВЕДЕНИЕ Ацетилхолиновые мускариновые рецепторы представляют собой группу белков, которые вовлечены в самые разные физиологические процессы. Hапример, они принимают участие в регуляции когнитивных процессов; оказывают влияние на работу желез внутренней секреции; управляют работой гладкой мускулатуры; а также контролируют двигательную активность [1]. Причём, разные варианты рецепторов имеют различную локализацию в тканях организма. Таким образом, мускариновые рецепторы являются важными биомишенями, ингибиторы которых рассматриваются как лекарственные средства для лечения целого спектра патологических состояний [2]. В этой связи становится особенно важным фактор селективности связывания того или иного соединения, для минимизации возможных побочных реакций в организме [3]. В настоящее время вычислительные методы широко используются для поиска молекулярных структур, обладающих биологической активностью по отношению к заданным рецепторам. Одним из ключевых направлений в это области является предсказание различных характеристических параметров для молекулы на основании данных молекулярного докинга и молекулярной динамики. Данный подход продемонстрировал высокую эффективность в более ранних работах [4]. Очевидно, что предсказание набора констант ингибирования (Ki) для определенного лиганда относительно максимально полного набора белков как потенциальных мишеней может стать инструментом, который, с одной стороны, может помочь найти высокоселективные структуры как прототипы для будущих лекарственных средств, а с другой - отбросить на ранних стадиях разработки структуры с потенциально широким спектром побочных явлений. Основной задачей данной работы было создание набора моделей для оценки параметров конкурентного ингибирования относительно метилскополамина произвольного лиганда к набору ацетилхолиновых мускариновых рецепторов M1, M2, M3 и M4. К сожалению, на момент выполнения работы 3D структура рецептора M5 (или гомолога достаточно близкого для успешного моделирования) была неизвестна. МАТЕРИАЛЫ И МЕТОДЫ 3D cтруктуры рецепторов и подготовка данных Из 5 ацетилхолиновых мускариновых рецепторов человека три (M1, M2 и M4) имеют известную 3D структуру, доступную в PDB [5,6] (табл. 1).
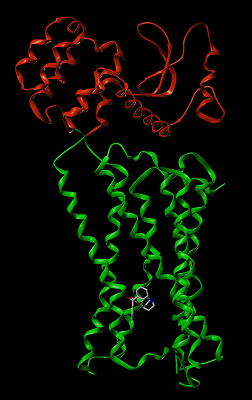
Кроме того, ещё один рецептор (M3) имеет известную структуру для рецептора крысы [7]. В настоящей работе мы будем рассматривать только эти 4 рецептора. Несмотря на то, что идентичность рецептора M5 в случае сравнения с M1 достигает 60% при минимальном пороге для успешного моделирования по гомологии в 35% [8], модель данного рецептора может вызвать много вопросов. Дело в том, что трёхмерная структура, строго говоря, получена для химерных, а не реальных рецепторов; в таком варианте внемембранная часть заменена на фрагмент другого белка, который, в свою очередь, позволяет сохранить архитектуру мембранной части рецептора [5-7]. В нашем случае при моделировании комплексов рецепторов с ингибиторами это не имеет значения, так как место связывания ингибитора существенно удалено от химерной части, и при моделировании она не влияет на ингибитор (рис. 1).
Только структура рецепторов M1 и M2 (использован файл 3UON из Protein Data Bank [9]) пригодна для молекулярного моделирования без модификаций структур. В случае рецептора M4 последовательность разрешена не полностью, в зонах петель, соединяющих основные альфа-спирали, имеются разрывы. Они были заделаны простым подбором петель, подходящих по конфигурации, средствами программы SYBYL-X [10]. Аминокислотные остатки, входящие в состав данных петель, также находятся далеко от места связывания, и их восстановление обеспечивает восстановление целостности структуры, что является необходимым условием для проведения молекулярной динамики, которая играет большую роль в нашей работе. Структура рецептора M3 (файл 4DAJ) была подвергнута виртуальному мутагенезу с целью восстановить на её основе последовательность (и структуру) рецептора человека. Следует отметить, что реальных аминокислотных замен меняющих, например, заряд или локальную гидрофобность (рис. 2), не так уж много, к тому же существенная их часть локализуется в зоне, заменённой на химерную часть, которая, естественно не модифицировалась.
Так как все имеющиеся структуры представляют из себя комплексы с известными ингибиторами, то подготовка включала в себя простую минимизацию в поле сил TRIPOS [10] для расчёта электростатических взаимодействий для рецептора. Для низкомолекулярных ингибиторов использовалась схема частичных зарядов из мерковского поля сил [11]. Данные по ингибиторам с известными значениями Ki. В настоящей работе используются 2 набора данных (табл. 2), отличительной особенностью которых является то, что значения Ki как минимум в 2/3 выборки доступны для всей линейки ацетилхолиновых мускариновых рецепторов человека.
Кроме того, обе выборки были получены на одном и том же наборе клеточных линий, и величина Ki оценивалась одним методом [12] по конкуренции с меченым метилскополамином. Выборка 1 [13] представляет собой коллекцию данных из различных источников, однако, оценка Ki, насколько можно судить по анализу источников, проводилась единообразно. Её достоинством также является относительно широкий диапазон данных - более 4-х логарифмических единиц. К сожалению, основной недостаток выборки 2 [14] – узкий диапазон значений Ki (меньше 2-х логарифмических единиц). В то же время, данные для второй выборки были получены одной группой в ходе выполнения единого проекта. Общим недостатком выборок являются их небольшие размеры. Процедура моделирования комплексов и расчёта параметров для создания предсказательных моделей. Комплексы ингибиторов с рецепторами моделировались по единой схеме:
Для построения предсказательных моделей использовались простые уравнения линейной регрессии. Так как в результате для таких уравнений было использовано 9 независимых переменных, то малые размеры выборок были серьёзным препятствием. Эту проблему преодолели, используя в качестве наблюдений все 25 состояний для любого из ингибиторов, полученных при динамике. Каждому из этих 25 состояний соответствовало одно и то же значение pKi. Для выполнения расчетов был использован гибридный высокопроизводительный вычислительный комплекс ФИЦ ИУ РАН [18] IBM Minsky (2xPower8, 4хTesla P100). Так как часть вычислений не могла быть выполнена на GPU, был написан набор макросов для балансировки нагрузки сервера. Среднее время расчётов на 1 комплекс составило 46 мин для вычислений на GPU и 4 ч на CPU. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ Основной проблемой при анализе результатов докирования стала проблема выбора «правильного» комплекса. Достоверного на 100% способа отбора не существует, к тому же, в ряде случаев процедура докирования вообще не нашла решения (табл. 2). Выбор по оценочной функции докинга или последующей оценке энергетических параметров, полученных методом MMPBSA, в данном случае не помогает из-за больших размеров белка, плотной упаковки в районе места связывания и имеющихся полостей по соседству. Единственный возможный путь в данном случае – применить отбор вариантов по подобию: имеется группа похожих по структуре лигандов из одного химического ряда, следовательно, структуры их комплексов должны быть относительно похожи. Учитывая, что в нашем случае структура комплекса подвергается длительной процедуре оптимизации, нас, в основном, интересовало, чтобы положение молекулы, полученное в результате докирования, занимало соответствующее место, а молекулы в пределах одного гомологичного ряда располагали общую часть относительно похоже, в надежде на то, что оптимизация потом «дотянет» лиганд до нужной конформации. В результате (табл. 3) были отброшены ещё несколько вариантов. В таблице 3 приведены параметры построенных корреляционных уравнений.
Уравнения «обучались» на наборе из 25 состояний для каждой из молекул выборки (общий вариант). Таким образом, даже при самом минимальном наборе молекул в выборке формально число наблюдений многократно превышало число независимых переменных (9). В тоже время, как при оценке качества обучения, так и при использовании тестовых выборок для каждой молекулы получали набор из 25 предсказаний, на основе которых вычисляли среднее значение. Предсказательную силу моделей оценивали путём перекрёстного предсказания между выборками 1 и 2. Сравнение зон предсказания (на рис. 3 для рецептора М3) показывает правильность сделанного предсказания. Та же картина характерна для всех рецепторов.
Было проведено также сравнение предсказательной силы уравнений при кроcс-рецепторном предсказании (табл. 4).
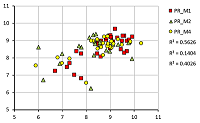
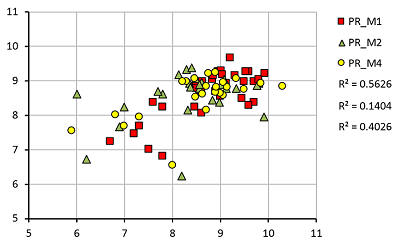
Однако удовлетворительного результата получено не было. Несмотря на то, что даже в этом случае можно различить слабые и сильные ингибиторы (рис. 4), достоверность таких предсказаний невысока.
Создание же объединённой выборки даже при использовании индикаторных переменных, характеризующих к какому рецептору относятся данные, не даёт при обучении удовлетворительного результата. Тем не менее, использование данных уравнений, рассчитанных для каждого из рецепторов, позволяет при некоторых априорных ограничениях предсказать pKi со средней точностью 0.65 логарифмической единицы. И таким образом возможно построить профиль действия любого соединения на ацетилхолиновые мускариновые рецепторы человека. При наличии же предполагаемого профиля действия становится возможным более эффективное планирование экспериментов по тестированию новых соединений и выявлению возможных побочных явлений на ранней стадии разработки лекарственных средств. БЛАГОДАРНОСТИ Работа выполнена в рамках государственного задания на 2018 год (тема № 0090-2017-0020). Подготовка и отладка программного обеспечения выполнялась при поддержке гранта РФФИ № 18-29-03100. ЛИТЕРАТУРА
|